Popüler

Bir çift düşünün. Evden çıkıp sinemaya gidiyorlar. Adam karısına geç hazırlandığı için kızıyor. Asansörde tartışarak iniyorlar.
Yolda trafik sıkışıyor. Adam bir yandan kendisini sıkıştıran araçlara bağırıp çağırıyor, bir yandan da geç kalmalarına sebep olan karısına saydırıyor.
Park yeri bulamayıp bir on dakika da öyle dolanıyorlar ve tam bir sinir harbi yaşıyorlar. Film de hoşlarına gitmiyor. Çıkışta bu sefer kadın, kötü bir film seçtiği için eşini suçluyor. Tartışarak eve dönüyorlar.
Şimdi gelelim sosyal medyaya.
Siz bu çiftin arkadaşı olduğunuzu düşünün. Evinizde pijamalarla huzur içinde oturuyorsunuz. Bu arada Instagram’a arkadaşınızın fotoğrafı düşüyor. İki tane gülümseyen yüz, kucakta kocaman bir patlamış mısır paketi, arka planda filmin afişi.
Fotoğrafın altında şöyle yazıyor;
“Harika bir bahar akşamı, enfes bir film, patlamış mısır ve aşkım.”
Cümlenin sonunda bir de kalp var. Moraliniz bozuluyor. “Ben evde atletle oturuyorum. Millet nasıl da eğleniyor!” diye canınızı sıkıyorsunuz.
İşte sosyal medyanın illüzyonu bu. Herkes ucu bucağı olmayan bir podyumda ha bire poz veriyor. Seyirciler de bu büyük kıyaslama oyununa ha bire özeniyor.
Sosyal medyada mutlu gözükmek için harcanan çok büyük bir gayret var. Ama ekranda bu gayret gözükmüyor.
Stanford Üniversitesinde konuyla ilgili çalışmalar yapan araştırmacılar işte bu durumlar için bir kavram geliştirmişler; “Ördek Sendromu.”
Ördekler gölün üzerinde hiçbir çaba sarf etmiyormuş gibi, rahat ve dingin bir şekilde süzülürler. Gölün altında kalan ayakları bir makine gibi çalışır ama dışarıdan bakınca hiç belli olmaz.
Sosyal medyada suyun altında kalan kısımlar da ekranda gözükse, inanın kimse moralini falan bozmaz.

Pompei, Vezüv yanardağına çok yakın bir yerleşim birimidir. Olay M.S. 80 yıllarında gerçekleşmiştir.
Yanardağ lav püskürtmeden önce zehirli bir gaz çıkartmıştır.

Bu gaz genzi yakan ve kısa sürede insanları öldürebilecek nitelikte bir gazdır. Olayın gece yarısı olması insanların bu gaza uykuda yakalanmasına ve kaçamamalarına neden olur.

Çoğu insan ve hatta şehirde yaşayan köpekler bir kaç dakika içinde ölür. Daha sonra şehre volkanın külleri dökülür. Bu küller şehrin üstünde üç dört metre bulacak biçimde birikir.

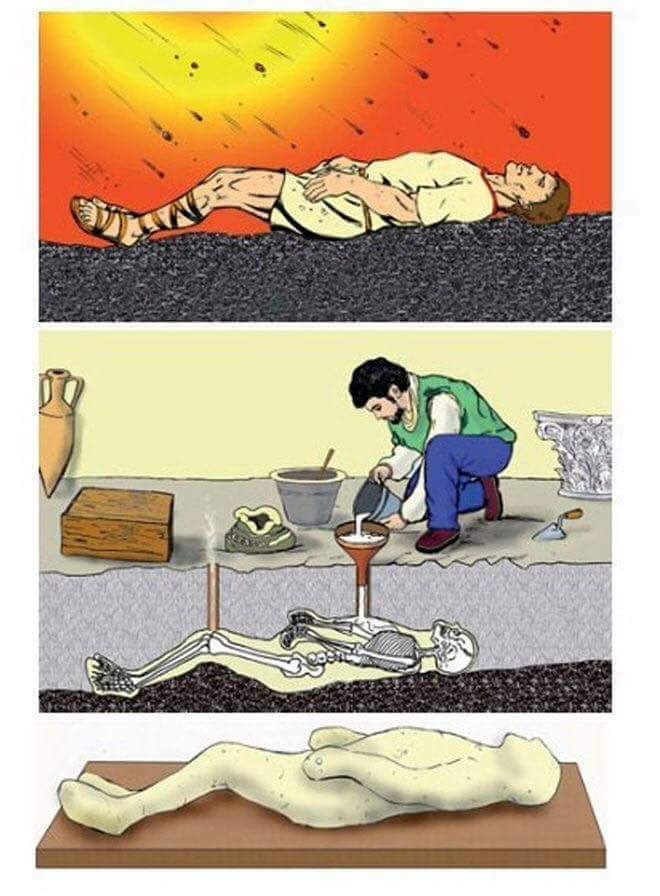
1900'lü yıllarda yapılan arkeolojik çalışmalarda bir arkeolog küllerin arasında biçimli boşlukların olduğunu fark eder. Bu türden bir boşluğa sıvı alçı dökerek kalıbını çıkartır, çıkan sonuç öldükten sonra üstüne kül biriken canlılar zamanla yok olmuşlar ama bedenlerini çevreleyen kül tabakasının sertleşmesiyle şekilleri korunmuştur.

Bugün Napoli'de yaşayan birine yanardağın lavıyla insanların taşlaştığını söylerseniz ya da ilahi bir gücün onları taş ettiğini söylerseniz siz gülerek onların birer alçı olduğunu söyler.

Olayı bilmeyenler için birer muamma olan bu 'taşlaşmış' insanlar aslında tamamen zehirli gazla ölüp üstüne kül biriken insanların neredeyse 1800 yıl sonra bulunup alçıdan kalıplarının çıkartılmasından ibarettir.

1. Akşemseddin: Pasteur ’dan 400 sene önce mikrobu buldu...

2. Ali Kuşçu: Büyük astronomi bilgini. İlk defa ayın şekillerini anlatan kitabı yazdı...

3. Ebul-Vefa: Trigonometri’de tanjant, cotanjant, sekant, kosekantı bulan büyük alim...

4.Birûni: İlk defa dünyanın döndüğünü ispat etti...

5. Ebu Kâmil Şü’ca: Avrupa'ya matematiği öğretti...

6. Ebu Ma’şer: Med-Cezir (Gel-Git) olayını ilk o buldu...

7. Battâni: Dünyanın en büyük kaşifidir. Trigonometrinin kaşifi...

8. Câbir Bin Hayyan: Atom bombası fikrinin babası ve kimya biliminin atası büyük alim...

9. Cezerî: 8 asır önce otomatik sistemin kurucusu ve bilgisayarın babası...

10. Demirî: Avrupalılardan 400 sene önce zooloji ansiklopedisini yazdı...

11. Farabî: Ses olayını ilk defa fizîki yönden açıklamıştır. Sesin fizîki izahını ilk defa o yaptı...

12. Gıyâsüddin Cemşid: Matematikte ondalık kesir sistemini ilk o buldu...

13. İbn Cessar: Cüzzamın sebebini ve tedavisini 900 sene önce açıkladı...

14. İbn Hatip: Vebânın bulaşıcı bir hastalık olduğunu ilmi yoldan açıkladı...

15. İbn Firnas: Wright kardeşlerden bin sene önce ilk uçağı yapıp uçmayı gerçekleştirdi...

16. İbn Karaka: 900 sene önce harika bir torna tezgahı yaptı...

17. İbni Türk: Cebirin temelini atan bilginlerdendir...

18. İdrisî: Yedi asır önce bugünküne çok benzeyen dünya haritası çizdi...

19. İbni Sina: Eserleri Avrupa üniversitesinde 600 sene ders kitabı olarak okutuldu. Tıbbın babasıdır. AVRUPA ya göre adı AVICENNA’dır...

20. Kadızâde Rûmi: Yaşadığı asrın en büyük matematik ve astronomi bilginidir. Fizik kurallarını astronomiye uyarladı...

21. Kambur Vesim: Verem mikrobunu R.Koch’tan 150 sene önce keşfetti...

22. İbnün Nefis: Avrupalılardan üç asır önce küçük kan dolaşımını keşfetti...

23. Piri Reis: 400 sene önce bugünküne en yakın dünya haritasını çizdi...

Gece saat 22:00'dan sonra, alkol almak ve üstüne veresiye yazdırmak istiyorum dayının komik ikna etmeye çalışma videosu.

Pek değerli Albert Einstein’ın özel görelilik kuramına göre Uzay’da herhangi bir cisme doğru bir hareketimiz olursa hızımızla doğru orantılı şekilde cismin gelecekteki durumuyla aynı zamanda seyretmiş oluyoruz. Tam tersi vektörde ise geçmişiyle aynı zamanı paylaşıyoruz. Bu durum dünyanın iki ayrı ucunda olsak dahi hissedilemeyecek kadar küçük rakamlara tekabül ediyor. Zaten somutsal olarak istenilen hızlara çıkma olasılığımız da şuanki teknoloji ile zor görünüyor. Bu nedenle hissedemiyoruz.

Varlığından emin olduğumuz ama sayılarla ve yönlerle ifade edemediğimiz şeyler yok mu var. Sevgi mesela. Hadi sevgiyi ele alalım. Sevginin büyüklüğünün olduğu konusunda mutabık kalırsak. Üç büyüklükten herhangi birine yerleştirmeliyiz. Eğer biz “onu seviyorum” gibi bir cümle kurabiliyorsak yön belirtmiş oluyoruz ve bu vektörel bir büyüklük olarak tanımlanıyor ( Aslında matematiğin tanıyamadığı büyüklükler yönüne bakılmaksızın “Temel büyüklükler”‘e giriyor ama burada bilimsel bir makale yazmıyorum. İstediğim gibi sallayabilirim.)

Bu anlattıklarımı bir çatıda toplarsak birinin gönlüne ne kadar hızlı gidersek o kişinin geleceğinde bulunuyoruz ve bir insanın gönlünden ne kadar hızlı çıkarsak o kadar geçmişini yaşıyoruz.

Görür görmez vurulduğunuz birini unutmak o denli zorlaşıyor bu sebeple. Ve herhangi birinin gönlünden ne kadar hızlı çıkarsan o insan size o kadar tecrübesiz ve aptal karşılık veriyor haliyle.

İngilizler aşık olmak dememiş mesela aşka düşmek demiş ve bana göre muhteşem bir tabir kullanmış aşka dair. Aşka düşerken ölçülebilecek bir şey olmadığı için limit hız kurallarının olmaması gerekiyor.

Bu sebepledir ki bazı insanların geleceğine gideriz, bazı insanların geçmişinden çıkarız. Gelecek görmeden ona gitmek ya da geçmişini yaşamadan ondan vazgeçmek mümkün değildir.

Her şeyden öte gözlerine baktığınızda zaman sizin için farklı akmıyorsa hiçbir şey kalmamıştır sizde.

Eid Al-Adha(Kurban Bayramı) Müslümanların, dini bir görüm sonucu İbrahim'in oğluna cinayet girişimini, hayvanları öldürerek kutladıkları bir Müslüman bayramıdır.

1. Kuran da, İbrahimin Hikayesi

Kuranda, İbrahim'in oğluna karşı dini nedenlerle cinayet teşebbüsü şöyle anlatılır:

"Ey Rabbim! Bana salihlerden olacak bir çocuk bağışla.” Biz de ona uysal bir oğul müjdeledik. Çocuk kendisiyle birlikte koşup yürüyecek yaşa gelince İbrahim ona, “Yavrum, rüyamda seni kurban ettiğimi gördüm. Düşün bakalım, ne dersin?” dedi. O da, “Babacığım, emrolunduğun şeyi yap. İnşaallah beni sabredenlerden bulacaksın” dedi. Her ikisi de teslim olup onu alnı üzere yatırdı." Saffat 100-103

Kelimenin tam anlamıyla bir rüyada(في المنام) olduğu söyleniyor. İbrahim, oğlunu bir rüyaya dayanarak öldürmeye çalıştı ve Müslümanlar bu olayı kutladılar.

2. Hadislerde

Hayvanları öldürmek zorundasınız.

"Bera bin Azib tarafından anlatılana göre: "Kurban bayramı namazında Peygamber efendimizi hutbe okurken işittim. Şöyle diyordu: “Bugün ilk yapacağımız şey bayram namazı kılmak, sonra dönüp kurbanlarımızı kesmektir. Kim böyle yaparsa bizim sünnetimize uygun hareket etmiş olur." Sahih Buhari 2:15:71

Ve biraz müzik var:

Muhammed müzik aletlerini ve şarkıcı kızları yasakladı. Ve bununla ilgilenenlerin maymunlara ve domuzlara dönüşeceğini söyledi.

Ebu Malik El-Eşari tarafından anlatılana göre Allahın Resulü şöyle söyledi: "Benim ümmetimden bazıları başka isimler altında mutlaka içki içeceklerdir. Başuçlarında çalgılar çalınacak ve kadın sanatçılar şarkı, türkü söyleyecekler. Allah onları yere batırsın! Ve onlardan domuzlar, maymunlar yapsın!" Sünen-i İbn Mace 5:36:4020

Ama İbrahim'in cinayet teşebbüsünü kutlamaya gelince müzik kullandı.

"Aişe tarafından anlatılana göre: "Bayram günü iki cariye, kahramanlık şiirlerini def çalarak şarkı söylüyorlardı. Resulullah yatağına yatıp yüzünü çevirdi, sonra babam(Ebu Bekir) içeri girdi. "Bu ne hal, Resulullah’ın huzurunda şeytanın düdüğü ve sesi ne arıyor?" diye beni azarlayınca, Resulullah "Bırak onları, her milletin bir bayramı vardır, bu da bizim bayramımızdır." buyurdu. Babam başka şeyle meşgulken, cariyelere işaret ettim, dışarı çıktılar." Sahih Buhari 2:15:72

Ve kafirleri öldür:

"Ebu Said el-Hudri tarafından anlatılana göre: "“Rasulullah Kurban ve Ramazan Bayramı günlerinde musallaya çıkardı. Orada önce namazla başlardı. Namazı kıldırıp selamı verince cemaat namaz kıldığı yerde otururken ayağa kalkar ve onlara yönünü dönerdi. Şayet kendisinin bir müfreze gönderme ihtiyacı olursa bunu insanlara söylerdi. Veya başka bir şeye ihtiyacı olursa onu insanlara emrederdi..." Sahih Buhari 2:15:76

SONUÇ

İbrahim, gördüğü bir rüyaya dayanarak kendi oğlunu öldürmeye karar verdi. Ve Muhammed bu olayı İslamda haram olan müziği dinleyerek, hayvanları öldürerek ve insanları öldürerek kutlardı.